1. Задание № 31 

Сложность: I
Классификатор алгебры: 13\.1\. Область определения функции
Область определения функции
i
Функция 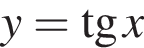 не определена в точке:
не определена в точке:
1) 
2) 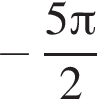
3) 
4) 
5) 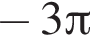
Решение. Функция 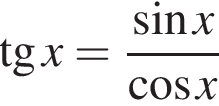 не определена, когда
не определена, когда 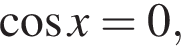 т. е. при
т. е. при 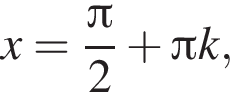 где
где ![]() Таким образом, она не определена в точке
Таким образом, она не определена в точке ![]()
Правильный ответ указан под номером 2.
Ответ: 2
31
2
Сложность: I
Классификатор алгебры: 13\.1\. Область определения функции
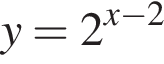
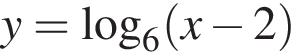


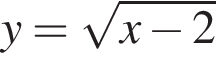
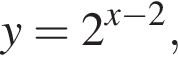
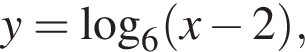
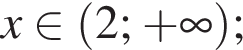
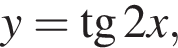
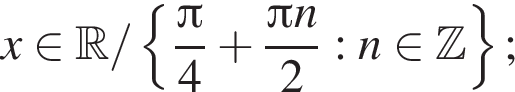

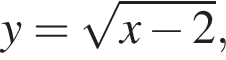
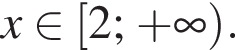
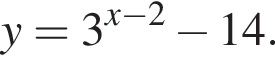
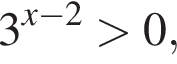 то y > −14. Следовательно, −16 и −14 не принадлежат множеству значений исходной функции.
то y > −14. Следовательно, −16 и −14 не принадлежат множеству значений исходной функции.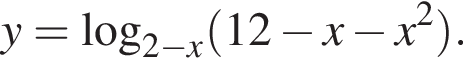
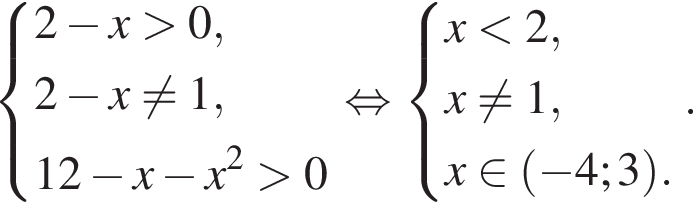
 Их сумма:
Их сумма: 
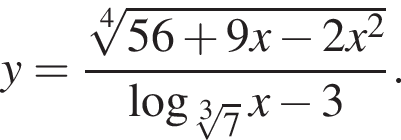
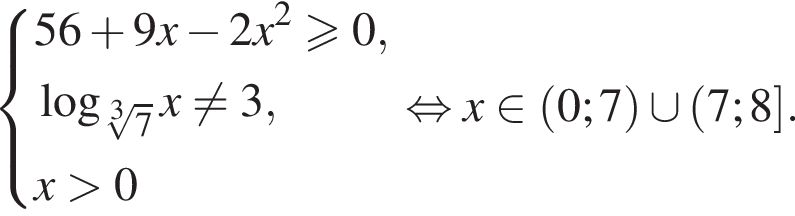
 Укажите номера верных утверждений.
Укажите номера верных утверждений.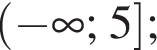
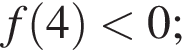

 — функция не является четной или нечетной.
— функция не является четной или нечетной.